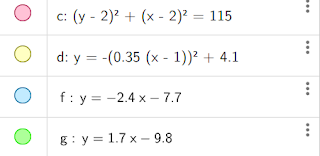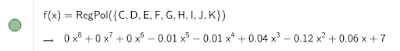Henri Matisse (1869-1954), pittore francese, è il rappresentante più noto del fauvismo. Il movimento dei Fauves è il contributo francese alla nascita dell’espressionismo. Ma, rispetto agli analoghi movimenti tedeschi, connotati da atmosfere fosche e contenuti drammatici, il fauvismo rappresenta una variante «mediterranea» e solare dell’espressionismo. La vivezza coloristica, che è il vero tratto caratteristico di questo movimento, esprime un’autentica «gioia di vivere» che resterà costante in tutta la produzione di Matisse.
Il gruppo dei Fauves, pur non essendo un movimento organico, si riconosceva in alcune comuni convinzioni: soprattutto, il dipinto deve comporsi unicamente di colore. Senza ricercare la verosimiglianza con la natura, il colore deve nascere dal proprio sentire interiore. Il colore viene quindi svincolato dalla realtà che rappresenta ma esprime le sensazioni che l’artista prova di fronte all’oggetto che riproduce.
Il fauvismo rappresenta la prima vera rottura con l’impressionismo ed è la prima esperienza moderna che svincola il rapporto tra colore reale delle cose e colore impiegato per la loro rappresentazione pittorica. I presupposti per queste scelte derivarono dalla conoscenza della pittura di Cezanne, Van Gogh e Gauguin. Da Cezanne presero l’idea della scomposizione e ricomposizione non prospettica delle forme, e da Van Gogh e Gauguin l’uso del colore come autonoma espressione interiore.
Henri Matisse iniziò la sua attività di pittore a Parigi intorno al 1890. Studiò presso il pittore simbolista Gustave Moreau e presso l’École des Beaux-arts di Parigi. In questi anni conobbe Albert Marquet, André Derain e Maurice de Vlaminck. Dalla loro amicizia nacque il gruppo dei Fauves. La loro prima comparsa pubblica avvenne nel 1905 al Salon d’Automne.
Lo stile di Matisse già si definisce in questa fase della sua attività. I suoi quadri sono tutti risolti sul piano della bidimensionalità, sacrificando al colore sia la tridimensionalità, sia la definizione dei dettagli. L’uso del colore in Matisse è quanto di più intenso è vivace si sia mai visto in pittura. Usa colori primari stesi con forza e senza alcuna stemperatura tonale. Ad essi accosta i colori complementari con l’evidente intento di rafforzarne il contrasto timbrico. Ne risulta un insieme molto vivace con un evidente gusto per la decoratività.
La sua attività pittorica si svolse per decenni, nel suo quieto ambiente familiare, lontano dai clamori della vita mondana. Svolse la sua ricerca portando il suo stile ad un affinamento progressivo fino a farlo giungere, in tarda età, alle soglie dell’astrattismo. Ma senza mai perdere il gusto per la forza espressiva del colore.
|
Nel Musée Matisse abbiamo trovato quest'opera, e abbiam potuto riscontrare una funzione:
La funzione è una funzione polinomiale intera con dominio R di sesto grado, la funzione non è nè pari nè dispari, non sono presenti astinoti.















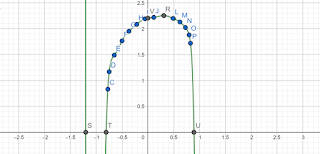


 ;-1,2]
;-1,2]