Pi Greco - Il Teorema Del Delirio
Maximilian Cohen, matematico geniale quanto eccentrico, soffre di continue emicranie causate dall'aver guardato direttamente il sole a 6 anni e, per ridurre il dolore, è costretto a fare un uso massiccio di analgesici. Uomo solitario, vive quasi in reclusione nel suo appartamento-laboratorio e il suo unico amico è il professor Sol
Robeson. Max crede in alcuni principi che regolano la sua vita: la matematica è il linguaggio della natura; ogni cosa esistente può essere spiegata e rappresentata con i numeri; in qualsiasi situazione, se analizzata a fondo, emergono degli schemi.
Sulla base di tali principi, Max cerca di ottenere uno schema che gli permetta di predire le quotazioni della borsa. La sua ricerca lo porta ad essere oggetto di pericolose attenzioni da parte di alcuni emissari di un'azienda quotata a Wall Street, la quale spera di speculare sulle eventuali scoperte di Max e che pertanto si spinge fino a sponsorizzarlo e minacciarlo per incentivare le sue ricerche. Il protagonista, inoltre, entra in contatto con un ebreo ortodosso studioso della Torah, che gli spiega come ad ogni lettera dell'alfabeto ebraico corrisponda un numero: a questo punto il misticismo cabalistico e le credenze ebraiche si fondono con ciò che Max, ebreo egli stesso, ritiene puro e razionale.
Parte delle 216 Cifre
Quando finalmente Max sembra essere riuscito nella sua impresa, il suo computer si guasta irreparabilmente, non prima, però, di aver stampato una sequenza di 216 cifre. A questo punto ne parla con il suo amico Sol, che gli spiega di essersi già imbattuto in un caso del genere quando da giovane faceva ricerche sul pi greco; il suo consiglio tuttavia è di desistere da ulteriori ricerche, perché la sua sanità mentale è a rischio. Poco dopo Max viene rapito e condotto a forza al cospetto del rabbino Cohen, suo omonimo: questi, dapprima apparentemente benevolo, gli spiega che il vero nome di Dio altro non è che la traslitterazione della serie numerica da lui scoperta. Alla fine del film Max parla con la bambina che di solito gli proponeva calcoli complicati quando lo incontrava sulla soglia di casa sua: egli non riesce a calcolare una moltiplicazione e, forse proprio per questo, lo si vede finalmente sorridere. Il film si chiude con un altro quesito posto da parte della bambina, cioè la divisione tra 748 e 238, il cui risultato, non svelato, è proprio 3,14 (la frazione è uguale a pi greco solo per due decimali, anche perché essendo irrazionale non esistono due interi che divisi tra loro diano π).
- "16 e 23, risultati: secondo Euclide, le NTC domani arriveranno a 100. Bella scommessa. Altre interessanti anomalie. Sempre secondo il vecchio Euclide, le PRONET si fermeranno a 65 e un quarto. Non capisco come. (Maximilian)"
- "10 e 28, risultato. Solo stronzate. Secondo Euclide le AAR arriveranno a 6 e mezzo. Ma se è da 20 anni che non scendono al di sotto di 40! Possibile spiegazione? L'errore umano. (Maximilian)"
https://it.wikiquote.org/wiki/Π_-_Il_teorema_del_delirio
"Euclide: 94143243431512659321054872390486828512913474876027 67195923460238582958304725016523252592969257276553 64363462727184012012643147546329450127847264841075 62234789626728592858295347502772262646456217613984 829519475412398501 "
http://aforismi.meglio.it/frasi-film.htm?n=PI+Greco+-+Il+teorema+del+delirio
Numero perfetto
In matematica, un numero naturale  si dice perfetto quando
si dice perfetto quando  dove la funzione
dove la funzione  è lafunzione sigma, cioè la funzione che fornisce la somma dei divisori positivi di
è lafunzione sigma, cioè la funzione che fornisce la somma dei divisori positivi di  . Poiché fra i divisori positivi di
. Poiché fra i divisori positivi di  c'è
c'è  stesso, questo equivale a dire che
stesso, questo equivale a dire che  è uguale alla somma dei suoi divisori propri.
è uguale alla somma dei suoi divisori propri.
 si dice perfetto quando
si dice perfetto quando  dove la funzione
dove la funzione  è lafunzione sigma, cioè la funzione che fornisce la somma dei divisori positivi di
è lafunzione sigma, cioè la funzione che fornisce la somma dei divisori positivi di  . Poiché fra i divisori positivi di
. Poiché fra i divisori positivi di  c'è
c'è  stesso, questo equivale a dire che
stesso, questo equivale a dire che  è uguale alla somma dei suoi divisori propri.
è uguale alla somma dei suoi divisori propri.
Ad esempio, il numero  , divisibile per
, divisibile per  è un numero perfetto: lo stesso per
è un numero perfetto: lo stesso per 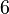 che è divisibile per
che è divisibile per  ,
,  e
e  .
.
 , divisibile per
, divisibile per  è un numero perfetto: lo stesso per
è un numero perfetto: lo stesso per 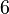 che è divisibile per
che è divisibile per  ,
,  e
e  .
.

- Cenni storici
I numeri perfetti furono inizialmente studiati dai pitagorici. Un teorema enunciato da Pitagora e dimostrato da Euclide rivelò che se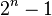 è un numero primo, allora
è un numero primo, allora  è perfetto. SuccessivamenteEulero dimostrò che tutti i numeri perfetti pari devono essere di tale forma. I numeri nella forma
è perfetto. SuccessivamenteEulero dimostrò che tutti i numeri perfetti pari devono essere di tale forma. I numeri nella forma 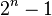 che sono primi sono detti primi di Mersenne. Si dimostra facilmente che se
che sono primi sono detti primi di Mersenne. Si dimostra facilmente che se  non è primo allora non lo è neanche
non è primo allora non lo è neanche 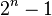 .
.
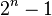 è un numero primo, allora
è un numero primo, allora  è perfetto. SuccessivamenteEulero dimostrò che tutti i numeri perfetti pari devono essere di tale forma. I numeri nella forma
è perfetto. SuccessivamenteEulero dimostrò che tutti i numeri perfetti pari devono essere di tale forma. I numeri nella forma 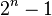 che sono primi sono detti primi di Mersenne. Si dimostra facilmente che se
che sono primi sono detti primi di Mersenne. Si dimostra facilmente che se  non è primo allora non lo è neanche
non è primo allora non lo è neanche 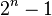 .
.
I numeri perfetti godevano di una particolare importanza nella cultura ebraica come dimostra il fatto che, secondo l'ebraismo, il Mondo era stato creato in 6 giorni e il calendario ebraico si basava sul mese lunare, di 28 giorni. Le proprietà matematiche e religiose di questi numeri perfetti vennero sottolineate in seguito anche da alcuni commentatori cristiani. Nel suo trattato "La Genesi alla lettera", libro IV, par.7,14, Sant'Agostino scrisse: "Sei è un numero perfetto in sé stesso, e non perché Dio ha creato tutte le cose in sei giorni. Anzi è vero l'opposto: Dio ha creato tutte le cose in sei giorni proprio perché questo è un numero perfetto".
Per le conoscenze attuali a tal proposito clicca qui:https://it.m.wikipedia.org/wiki/Numero_perfetto
Claudia Massarella



Lavoro approfondito e interessante, peccato alcuni problemi nella formattazione.
RispondiElimina